| Issue |
Apidologie
Volume 40, Number 6, November-December 2009
|
|
|---|---|---|
| Page(s) | 634 - 650 | |
| DOI | https://doi.org/10.1051/apido/2009062 | |
| Published online | 14 October 2009 | |
Original article
Complex structure of pollinator-plant interaction-webs: random, nested, with gradients or modules?*
Structure complexe des réseaux d’interactions plantes-pollinisateurs: au hasard, à emboîtements, avec gradients ou modules ?
Komplexität eines Bes- täuber-Pflanzen-Netzwerkes: zufällig, geschachtelt, mit Gradienten oder Modulen?
1
Ecology, University of Osnabrück, Barbarastr. 13, 49069
Osnabrück, Germany
2
Vegetation Ecology, Darmstadt University of Technology,
Schnittspahnstraße 4,
64287
Darmstadt, Germany
Corresponding author: A. Kratochwil,
Kratochwil@biologie.uni-osnabrueck.de
Received:
25
October
2008
Revised:
22
March
2009
Accepted:
7
April
2009
We analysed the interaction web of a plant-bee pollinator community (Hymenoptera: Apidae, honeybees excluded) for two years. Based on the ordination of the incidence matrix, both webs showed coherence and clumping but no species turnover. While this may indicate a moderate set of nested subsets and sub-communities, further analysis of nestedness did not reveal uniform results. A null-model analysis of different nestedness metrics showed no evidence despite the asymmetric structure of bipartite graphs. However, further analysis revealed significant modularization within the community with connected hub species within modules and module-interlinking connector species. The web is characterized by 4–6 dominant connector plant species, representing four main flower types. The pattern depends on the year. DCA demonstrates that the connector plant species support resources for bees of different body sizes and behaviour. The pattern is characterized by modularity and the existence of specific connector plant species.
Zusammenfassung
An einem Modellökosystem konnte innerhalb eines Zeitraumes von zwei Jahren das Wildbienen-Nahrungspflanzen-Netzwerk (Hymenoptera Apoidea) analysiert werden. Die Honigbiene (Apis mellifera) blieb dabei unberücksichtigt. Folgende Methoden kamen zum Einsatz: Nested-Subset-, Gradienten- (Clements, Gleason und Tilman) und Modularitätsanalysen. Wir untersuchten das Netzwerk auf Kohärenz, Kompartimentierung und Schachtelung und kamen zu dem Ergebnis, dass unser System modularisiert und teilweise auch schwach geschachtelt ist. Geschachtelte Gemeinschaften von Höheren Pflanzen- und Wildbienenarten garantieren das Überleben seltener und spezialisierter Arten. Nach der Nested-Subset-Theorie nutzen seltene und spezialisierte Blütenbesucher weitverbreitete und auf einen großen Blütenbesucherkreis eingerichtete Pflanzenarten. Das Gleiche gilt für seltene und im Blütenbesuch spezialisierte Pflanzenarten. Weiterführende Analysen zum Nachweis von Nested-Subset-Strukturen erbrachten in der Mehrzahl den Hinweis, dass das gesamte Nahrungsnetz nicht geschachtelt ist. Der bipartite Graph belegt eine asymmetrische, teilweise geschachtelte Netzwerk-Struktur, wobei seltene Bienenarten und solche mit Präferenzen für Korbblütler (Asteraceae) und Schmetterlingsblütler (Fabaceae) die häufigeren Pflanzenarten oder solche mit einem breiten Blütenbesucherkreis nutzen. Seltene Pflanzenarten werden durch häufige, im Blütenbesuch sich generalistisch verhaltende Wildbienenarten besucht. Eine Nullmodell-Analyse erbrachte für den bipartiten Graphen des Jahres 2005 jedoch keine signifikante Schachtelung für das Gesamtsystem. Dagegen konnte ein signifikantes modularisiertes Muster festgestellt werden mit einzelnen Arten, die innerhalb eines Moduls eine hohe Konnektivität besitzen (,,hub species“), aber auch solchen, die zwischen den Modulen vermitteln (,,connector species“). In der Regel wird das Netzwerk durch 4-6 dominante Pflanzenarten charakterisiert, die die Rolle von ,,hub“ oder ,,connector species“ einnehmen. Das Muster variiert in den beiden Jahren bezüglich der Anzahl der Module und Bindungen zwischen den Arten. Die dominierenden ,,hub“- und ,,connector“-Pflanzenarten treten jedoch in beiden Jahren auf. Eine multivariate Analyse zeigt, dass die ,,hub“ und ,,connector species“ vier Haupt-Blütentypen repräsentieren. Diese Blütentypen gewährleisten, dass Wildbienenarten mit unterschiedlicher Körpergröße und unterschiedlichem Ernährungsverhalten adäquate Ressourcen nutzen können. Modularität und Anwesenheit spezifischer ,,hub“ und ,,connector species“ kennzeichnen die hier vorliegende Netzwerk-Struktur. Im Gegensatz zu theoretischen Netzwerken (zufällig, mit Gradienten, modularisiert) zeigt dieses reale Wildbienen-Nahrungspflanzen-Netzwerk einen hohen Grad an Komplexität mit Übergängen zwischen verschiedenen Netzwerk-Typen. Damit wird das Aussterben lokal seltener Bienenarten minimiert. Im Blütenbesuch spezialisierte Wildbienen-Arten kommen nur in geringen Abundanzen vor. In der überwiegenden Mehrzahl nutzen sie im Gebiet weit verbreitete, sowie arten- und individuenreiche Pflanzenfamilien (Asteraceae, Fabaceae). Das Netzwerk wird von polylektischen Bienenarten dominiert. Im Gegensatz zu Ergebnissen aus der Literatur, in denen Nestedness mit Systemstabilität in Verbindung gebracht wird, ist unser Netzwerk primär durch Modularität charakterisiert, wobei aber eine partielle Schachtelung in dieses System integriert ist.
Key words: coherence / nested subsets / bipartite web / modularity / real network structure
Mots clés : cohérence / sous-ensemble imbriqué / réseau bipartite / modularité / Apidae
Schlüsselwörter: Kohärenz / Nested-Subset-Analyse / bipartites Netzwerk / Modularität / reale Netzwerkstrukturen
© INRA/DIB-AGIB/EDP Sciences, 2009
1. INTRODUCTION
On a community level, interactions between plant species and flower-visiting species can be characterized as “plant-flower-visitor networks” (Dupont et al., 2003). There have been many studies on such networks, mostly covering one or parts of one season and including only selected visited plant species or selected flower-visiting animals (Kratochwil, 1984; Memmott, 1999; Olesen et al., 2002; Jordano et al., 2003; Philipp et al., 2006; Forup et al., 2008). In recent times, investigations have focused more intensively on the structure of flower-visitor network structures, such as nestedness, compartmentation, or modularity (Bascompte et al., 2003; Ollerton et al., 2003; Lewinsohn et al., 2006; Olesen et al., 2008).
Bascompte et al. (2003), Bascompte and Jordano (2006), and others point out that mutualistic networks are generally nested. This was shown by nested subset analyses based predominantly on the concept of the “Nested Temperature Calculator Program” (NTC) elaborated by Atmar and Patterson (1993, 1995). The matrix temperature T is a percentage that measures how much the presence-absence matrix departs from perfect nestedness. It is used in certain disciplines (e.g., biogeography) to quantify the effects of fragmentation on metacommunities (Ganzhorn and Eisenbeiß, 2001; Armbrecht et al., 2001; Fischer and Lindenmayer, 2005a) or spatio-temporal changes of communities (Bloch et al., 2007). According to Bascompte et al. (2003) and Dupont et al. (2003), plant species may be regarded as “resource islands” for flower-visiting species, thus enabling a nested subset analysis of the network of plant- and flower-visiting species. For this purpose, a presence-absence matrix is established, with bee species aligned in columns (called “species”) and plant species in rows (called “islands”). Many studies use NTC as “ideally suited to explore various features of nestedness” and hence used as the basis for far-reaching conclusions from the assumed nestedness (e.g., Ibáñez et al., 2005).
The demonstration of nestedness is interpreted as follows: bipartite networks are nested if those species with fewer interactions are associated with a subset of species that interact with the most connected ones (Bascompte et al., 2003). Therefore, plant species that are characterized by only limited interaction processes are often associated with those flower visitors that are widespread, abundant, and generalists. In contrast, specialized flower visitors (oligolectic species) are often closely connected with widespread and abundant plant species, which are visited by broad spectra of bees and are characterized by a high degree of interaction. Moreover, bee and plant generalists tend to interact with other generalists, thus creating a close interactive network (Lewinsohn et al., 2006). Such asymmetric structures in plant-visitor interactions seem likely to be the rule (Ashworth et al., 2004; Vázquez and Aizen, 2004; Blüthgen et al., 2007; Olesen et al., 2008). Many such networks most probably depend on generalists (Waser et al., 1996; Memmott, 1999).
It is possible to quantify the pattern of nestedness with different programs, such as NTC (Atmar and Patterson, 1995), Binmatnest (Rodriguéz-Gironés and Santamaría, 2006), Nestedness (Ulrich, 2006a). Alternatively, one can use discrepancy indices (e.g., “BR”; Brualdi and Sanderson, 1999), a suitable indicator for the presence of nestedness (Ulrich and Gotelli, 2007), or “d1” (Greve and Chown, 2006), all of which take into consideration the occurrence of “singletons” (= data occurring only once in a matrix) leading to higher nestedness values. Recently, a new metric (“NODF”) has been proposed by Almeida-Neto et al. (2008) quantifying neglected properties of nestedness (Ulrich, 2006b).
Besides nestedness, a non-random interaction matrix can also be detected as a gradient, a compartmented, or a combined structure. Leibold and Mikkelson (2002) present methods for analysing the species pattern by coherence, species turnover, and boundary-clumping analysis to detect random patterns (Simberloff, 1983), checkerboards (Diamond, 1975), nested subsets (Patterson and Atmar, 1986), or different gradient types. Clementsian gradients (Clements, 1916) are characterized in discrete subcommunities in a web that replace each other as a group, Gleasonian gradients (Gleason, 1926) result in species turnover with random arrangement of species ranges along the gradient, and Tilmanian gradients (Tilman, 1982) exhibit no discrete communities but arrange species more evenly than expected by random chance.
It is possible to visualize and test patterns by bipartite networks, co-occurrence analysis (Muller, 2008; Olesen et al., 2008), or multivariate sets (Lewinsohn et al., 2006; Almeida-Neto et al., 2007). Here, we use a data set sampled in a model ecosystem: species-rich sand grassland of the temperate zone. If networks are not nested, the consequences for system stability are serious because such non-nested systems should be highly vulnerable against disturbances. However, the ecological significance of nestedness has been disputed (Blüthgen et al., 2007) since it might be seen as a derived property of the bipartite network rather than a first-order property (Dormann et al., 2009).
The questions we pose here are as follows: (1) Are the network structures within the studied plant-bee webs distributed randomly, nested, or characterized by a gradient (and, if so, by a Clementsian, Gleasonian, or Tilmanian gradient)? (2) Is it possible to detect modularity in this pollination network? (3) Which functional traits (e.g., use of specific flower types, pollen-collecting structures, or body size) determine the community structure of the bee web?
2. MATERIALS AND METHODS
2.1. Study area
The study areas are situated in the northern Upper Rhine Valley near Darmstadt (Germany) in two nature protection areas (70 ha, 8° 35’ E, 49° 51’ N; 45 ha, 8° 34’ E, 49° 50’ N). The vegetation in both study areas is characterized by plant communities of sandy ecosystems (Beil et al., 2008) and dominated by important flower resources for bees (e.g., Echium vulgare, Helichrysum arenarium, Hieracium pilosella, Potentilla argentea, Medicago minima). The meteorological conditions during the study periods 2004 and 2005 were slightly warmer and drier than the long-term data of mean annual temperature 9–10 °C and mean precipitation of about 700 mm/a (2004: 10.7 °C, 2005: 11.0 °C, annual average precipitation 2004: 556 mm and 2005: 524 mm; Walter and Lieth (1967), Deutscher Wetterdienst Frankfurt/Main Airport).
2.2. Study design and sampling
The study was conducted from April to September in 2004 and 2005 on 45 circular permanent plots with radius 8 m (36 in a 50 ha area, 9 in a 12 ha area of open sand vegetation). Both areas belong to a formerly large sand area which had been fragmented about 50 years ago. We used a grid system with minimum plot distances of 50 m. Both the community structure of vegetation and the bee community structure are well represented by this approach. For vegetation, we were able to compare the grid approach with vegetation maps of the area; the same is true for the distribution maps of single bee species (unpublished data). Additionally, the plots are far enough apart to avoid negative sampling effects. Flower-visiting bees (Hymenoptera Apoidea) were caught by sweep nets from flowers mainly once a week during a period of 15 minutes/plot in both years under sunny conditions, with no or only slight wind and temperatures exceeding 12 °C. Bee species that could clearly be identified in the field were not caught. The flower resource visited by each individual bee was recorded, and the plots were sampled in changing order. The semi-domesticated honey bee (Apis mellifera) was excluded. “Parasites” refer to bee species practicing nest parasitism (e.g., cuckoo bees). The vegetation of each plot was sampled using the cover-abundance scale of Barkman et al. (1964).
2.3. Data matrix
The data matrix includes the number of bees, the number of entomophilous plant species, and the number of interactions. In total, 1714 individual bees were recorded (2004: n = 1172; 2005: n = 542). The structure of the bee community in one year is regarded as a distinct data set, reflecting the environmental conditions of the current year and the year prior.
2.4. Testing coherence, species turnover, and boundary clumping
To identify gradients or compartments, we used the approach of Leibold and Mikkelson (2002). This method is based on ordination of the incidence matrix to identify the dominant axis of variation. “Coherence” represents the degree to which the web pattern can be collapsed into a single dimension. “Species turnover” describes the replacements and “boundary clumping” defines the species distribution along this dimension. All significance values are based on iterations (n = 100) of the respective null model. Significance in coherence but not in species-turnover indicates nested subsets, significance in coherence, turnover, and boundary clumping characterizes a Clementsian gradient, significance in coherence and turnover with a MorisitaIndex I > 1 characterizes a Gleasonian gradient, and significance in coherence and turnover but no significant boundary clumping characterizes a Tilmanian gradient. Checkerboards and random patterns show no significant coherence.
2.5. Additional analyses to test nestedness
The software Nestedness (Ulrich, 2006a) overcomes almost all deficiencies of NTC (Atmar and Patterson, 1995), which detects nestedness in many cases as an artefact (Fischer and Lindenmayer, 2002, 2005b; Rodriguéz-Gironés and Santamaría, 2006; Ulrich, 2006a; Ulrich and Gotelli, 2007; Almeida-Neto et al., 2007, 2008). Binmatnest (Rodriguéz-Gironés and Santamaría, 2006) introduces a new order for the isoclines as well as further null models and uses a genetic algorithm, but some fundamental problems are not solved. Therefore, we preferentially used the software Nestedness (using the fixed-fixed null model; W. Ulrich unpubl. data) but additionally NTC (Random00 model) and Binmatnest (null model Type I and Type II errors). The cells situated at the borderline were calculated in Nestedness on the basis of the matrix fill. The “Fixed row and column constraints sequential swap” accounts best for passive sampling (Ulrich, 2006a). The number of iterations for computing standard deviations of the null model is 1000. The minimum distance to borderline is 0.5, which means cells nearer to the borderline will be excluded from the computation of the matrix temperature. The matrix is packed according to matrix temperature. We quantify the pattern of nestedness with the discrepancy index BR of Brualdi and Sanderson (1999) and the discrepancy value d1, which can be tested with the help of the software written by B. Harper for Greve and Chown (2006).
We used the new metric proposed by Almeida-Neto et al. (2008), which quantifies whether “fills” differ among columns and rows, and whether the presences in less-filled columns and rows coincide with those found in the more-filled columns and rows. This test was conducted with the programs CoOccurrence (Ulrich, 2006b) and Aninhado 3.0 (Guimarães and Guimarães, 2006) with fixed-fixed null model for randomization: random sampling according to the observed frequencies of occurrence (1000 iterations).
2.6. Bipartite graph: Interaction structure, linkage levels, abundance, degree of specialization
The bipartite graph presents species in columns or rows facing each other. The interactions are drawn as links and grouped by the number of interactions in decreasing order. For measuring the degree of generalization, linkage levels (ln) of plant (P) and bee species (B) were assessed (Olesen et al., 2002; Dupont et al., 2003). Linkage levels characterize the number of interactions per species (linkage level Lm of a bee species m is the number of plant species visited by m, linkage Ln of a plant species n is the number of bee species visiting n). For comparisons, the linkage level was standardized as relative linkage of bee species lm = Lm/P and relative linkage of plant species ln = Ln/B. Species with high linkage levels utilize more species than do species with low linkage levels. Spearman’s Rank-Correlations were used to analyze possible correlations between the degree of generalization (“linkage level”) and abundance. The distribution of a species is documented by the number of plots on which the species was detected. The degree of specialization in plant species is characterized by their flower type. For bee species, we differentiated polylectic and oligolectic species (as well as cuckoo bees) and three body-size groups.
For bee species, Mann-Whitney-U tests were used to detect differences in interaction number (I) and distribution frequency (D) between polylectic and oligolectic species, whereas plant species’ flower types were tested with a one-way-analysis of variance (ANOVA) followed by Tukey post-hoc tests and Kruskal-Wallis tests when data were not normally distributed or satisfied variance assumptions. Data sets were always log (x+1) transformed. Statistical analysis was carried out using the program Statistica 6.0 for Windows.
We analysed the pattern of our webs with the Bipartite Package 0.73 of Dorman et al. (2008) and present the data set from 2005 (at present, the data set of 2004 was not suitable for the program; Gruber, unpubl. data). Three different null models with different constraints about marginal totals, dimensions, and connectance were calculated. The Patefield algorithm (null model 1) produces null models with marginal totals that are identical to those of the observed web. Thus the distribution of rare and common species is equal, but the number of links is usually reduced compared to the observed matrix. Null model 2 (Shuffle) keeps the number of links constant but shows variation in the marginal totals. Finally, the Swap-algorithm (null model 3) keeps the marginal totals and the number of links identical to those of the observed matrix. To check for significance of the matrix temperature (degree of nestedness) between the observed data and the null models, a genetic algorithm with 2000 generations was used while the number of calculated null models per class was fixed to 100. Calculations were performed using the “nestedness” module provided by the bipartite library within R 2.8.1 (R Development Core Team, 2008).
2.7. Modularity
We tested modularity with the software NetCutter 1.0 (Muller, 2008). This software permits identifying and analyzing co-occurrence networks. NetCutter was individually modified by H. Muller for our tasks. We used edge-betweeness clustering proposed by Girvan and Newman (2002), which produces best results by visualization of the data sets like ours (Muller, unpubl. data). It is based on an iterative process of removing linkages to reach the highest modularity value. To prove significance, we randomized the original data set by edge-swapping (1000 iterations), tested 50 edge-swapping randomized graphs by edge-betweeness clustering, and calculated the modularity value including standard deviation for comparison with the real data set. Edge swapping is the best null model for co-occurrence analysis (Muller, unpubl. data), shuffling the linkages of a bipartite graph randomly (usually 100 iterations) while preserving the vertex degrees and avoiding linkage of the same plant species to the same bee species more than once. The graph structure and the presence of communities are visualized with CircleLayout. The size of the points representing the linked species grows in diameter with increasing linkage level.
2.8. DCA-analysis and functional group correlation
The functional relationships between plant and bee species are visualized by the detrended correspondence analysis (DCA) with PC-ORD 5.0 under “no downweighting of rare species”, “rescaling of axes”, “taking 26 segments”, and without singletons to eliminate multireferences and to clarify the graph. This linear ordination method is recommended in the case of gradient lengths more than 3 SD and a powerful multivariate tool (Kent and Coker, 1992; Ejrnaes, 2000). DCA with singletons produced the same result.
All methods are based on presence-absence data to guarantee comparability.
Coherence as indicated by the occurrence of embedded absences in ordinated matrices; species turnover as indicated by the number of times one species replaces another between two sites, and boundary clumping as indicated by Morisita’s Index (Leibold and Mikkelson, 2002).
3. RESULTS
3.1. Coherence, species turnoverand boundary clumping
Both data sets (2004, 2005) are significantly coherent and clumped according to the method of Leibold and Mikkelson (2002) but not characterized by species turnover (Tab. I). Combining these three results, the studied web pattern tends to be similar to a mixture between a nested subset pattern and a Clementsian gradient. Nested subset pattern (some species form a set of nested subsets) is detected by positive coherence plus negative turnover, and a Clementsian gradient by positive coherence plus positive boundaries (the argument positive turnover is not fulfilled).
Nested subset-analysis of the pollination web calculated via NTC (Atmar and Patterson, 1995), BINMATNEST (Rodriguéz-Gironés and Santamaría, 2006) and NESTEDNESS (Ulrich, 2006a), T = temperature in degrees, Trandom = randomized mean temperature (1000 iterations), N = degree of nestedness, P = level of significance.
Discrepancy indices: “BR” (Brualdi and Sanderson, 1999), “NODF” (Almeida-Neto et al., 2008) and “d1” (Greve and Chown, 2006), BRSim, NODFSim = randomized value (1000 iterations), P = significance level.
3.2. Additional analyses to test nestedness
The software Nestedness did not reveal significant nestedness in contrast to NTC and Binmatnest; only after masking (singletons of plant-bee interactions were removed from columns and rows), weakly significant nestedness was indicated for one year (Tab. II). The discrepancy index BR, d1, and NODF did not prove significant nestedness with one exception (NODF for the year 2005; see Tab. III). A second examination of the masked data concerning BR, d1, and NODF did not reveal any significant nestedness (Tab. III). The temperature values of NTC and Binmatnest showed clear differences. The temperature valuesdetermined by Binmatnest were always lower than those of NTC.
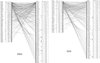 |
Figure 1 Web structure (bipartite graph) of the studied plant-bee system in 2004 (a) and 2005 (b). S = specialization (flower types: A = actinomorphic, Z = zygomorphic, AS= Asteroideae, CI = Cichorioideae; pollen collecting: P = polylectic, oligolectic in Asteraceae = AST, Boraginaceae = BOR, Fabaceae = FAB, Malvaceae = MAL, Salicaceae = SAL; C = cuckoo bees); Lm = plant linkage level; ln: relative plant linkage level; D = distribution; number of plots with occurrence; B = body size group (a = small [ < 10 mm], b = medium [ > 10–12 mm], c = large (> 12 mm)); Lm = bee linkage level; ln: relative bee linkage level lm. For abbreviations of plant and bee species, see Appendix. |
3.3. Bipartite graph: Interaction structure, linkage levels, abundance, degree of specialization
In 2004, 42 plant species were used as floral resources by 69 bee species (225 interactions); in 2005, 33 plant species were visited by 60 bee species (171 interactions). The relative linkage levels of plant species (ln) ranged from 0.01 to 0.38 in 2004 and from 0.02 to 0.42 in 2005, the relative linkage levels of bees (lm) from 0.02 to 0.52 in 2004 and from 0.03 to 0.33 in 2005 (Fig. 1a, b). Moreover, there were positive correlations between plant species abundance and ln (2004: n = 42; rS; P < 0.001; 2005: n = 33; rS; P = 0.102), which did not show significant values only in 2005. Also for bee species (bee species abundance and lm: 2004: n = 69; rS; P < 0.001; 2005: n = 60; rS; P < 0.001), the analyses revealed that the most common species also show the most frequent interactions with other species.
 |
Figure 2 Modularity graph (Software NetCutter 1.0; Muller, 2008) of 2004 and 2005, which is based on edge-betweenness clustering (further explanations see text). |
Concerning plant species, differences of interaction numbers were only detected between Asteroideae and Cichorioideae in 2004 (2004: ANOVA, df = 3, F = 3.389, P = 0.027; 2005: Kruskal-Wallis test: H3, P = 0.517). There was no difference in the presence of flower types (Kruskal-Wallis test: 2004: H3, P = 0.082; 2005: H3, P = 0.561).
The bipartite graphs of 2004 and 2005 (Fig. 1a, b) demonstrate a highly asymmetric pattern. Plant species with high interaction numbers were correlated with almost all bee species and vice versa. There were only a few exceptions (e.g., Senecio jacobaea, Vicia angustifolia or Lasioglossum minutissimum, and Nomada fulviventris). Within plant species, there was no correlation between distribution frequency and interaction number or flower type. In contrast, the highest interaction numbers in bee species were correlated with frequency. Polylectic bee species dominated in the group of species with many interactions and high distribution frequency. Oligolectic species (most of which occurred in only one or a few plots) showed a low number of interactions; the same was true for parasites. Plant species with low interaction number and frequency were visited mostly by those bee species with higher connectivity and wider distribution in the study area.
Temperature of nestedness analysed by The bipartite Package 0.73 (Dorman et al., 2008) for the data set of 2005: real data, null-model 1 (Patefield algorithm), null-model 2 (Shuffle) and null-model 3 (swap-algorithm).
The Patefield algorithm (null model 1) constructs networks that have significantly higher temperature (< 0.001) than the observednetwork (2005; see Tab. IV). This implies a lower degree of nestedness for null model 1. While still significantly different (P = 0.02 and P = 0.01, respectively) the Shuffle- (null model 2) and the Swap-algorithm (null model 2) generate marginally higher average matrix temperatures compared to the observed data of 39.5 and 38.5, respectively.
3.4. Modularity
The analysis of co-occurrence networks with NetCutter showed a modularized pattern of 5–7 in 2004 and only 2 modules in 2005 (Fig. 2a, b; Tab. V). Within one module, the species were strongly connected (hub species), between-module connector species interlinked the modules and more or less separated interactions.
 |
Figure 3 Detrended correspondence analysis of the plant-bee web 2004 with plant species (a) and bee species (b) plotted by PC-ORD 5.0 and characterization by flower types and bee body sizes. Key hub and connector plant species in bold and italics. For abbreviations of plant species, see Appendix. |
Modularity degrees of the real data sets (2004, 2005), of the 50 randomized graphs by edge-swapping (1000 iterations) according to NetCutter 1.0 (Muller, 2008).
Web modules in 2004 and 2005 according to NetCutter 1.0 (Muller, 2008) analysed with edge-betweeness clustering. In parenthesis species numbers; key hub and connector plant species in bold and italics. N = number of interactions. For abbreviations of plant species, see Appendix.
3.5. DCA-analysis and functional group correlation
The DCA diagrams for year 2004 (Fig. 3a, b) and 2005 (not printed) were based on the data set of the plant-bee web without singletons differentiated as plotted plant species (Fig. 3a) and plotted bee species (Fig. 3b). Figure 3a revealed two main and two further traits of plant species with different flower types. The left side of the graph represents plant species with relatively small, actinomorphic flowers (e.g., in 2004: Berteroa incana, Geranium molle, Alyssum alyssoides, Salsola kali, and in 2005: Potentilla tabernaemontani, P. argentea, Sedum acre) or inflorescences easily accessible to flower-visitors (Euphorbia cyparissias). Their flower visitors (Fig. 3b) were, above all, composed of bee species with small body sizes (Andrena, Lasioglossum, Halictus). These species are characterized by hind legs (coxa, femur) bearing hairs for pollen collecting. The right side of the graph (Fig. 3a) is dominated by plant species characterized by zygomorphic flowers (e.g., 2004: Stachys recta, Ononis repens, Salvia pratensis, Echium vulgare, and 2005: Echium vulgare, Vicia villosa). Their flower-visiting bee species (Fig. 3b) were of larger body size and have longer proboscises and other pollen-collecting structures (Bombus: hind-leg corbiculae; Megachile: hair brushes on abdominal tergites). Halictus species with larger body sizes also occur (e.g., Halictus quadricinctus, H. sexcinctus). The group with medium body size comprises species of Andrena, Osmia and Megachile with an intermediate position in the DCA. Moreover, there is another flower type, pseudanthia of the Cichorioideae, which is grouped on the left side of the DCA (Fig. 3a) and preferably visited by smaller bee species or in the case of Dasypoda hirtipes and Osmia spinulosa Asteraceae specialists (Fig. 3b). This group was only detected in 2004. Species visiting the Asteroideae type were grouped in the centre of the matrix. There was a compartmented gradient concerning flower type, body size of bees (which is mostly related with proboscis length), and pollen-collecting structures.
4. DISCUSSION
4.1. Coherence, species turnoverand boundary clumping
The metaanalysis presented by Leibold and Mikkelson (2002) demonstrates that in most cases community structures are characterized by coherence and not by randomness. Furthermore, communities tend to be either nested or characterized by a species turnover and to correspond either to a Clementsian or to a Gleasonian gradient. This can be shown for our data set (2004, 2005), which indicates significant coherence and a clumped pattern but no significance in species turnover. A moderate nested subset pattern is detected by positive coherence and negative turnover, and a Clementsian gradient is indicated by positive coherence and by positive boundaries, which means the existence of discrete subcommunities. The argument for “positive turnover” is not fulfilled. By the use of the methods summarized by Leibold and Mikkelson (2002), we are only able to characterize our web pattern as non-random, moderately nested, and “clumped”. With additional methods, the structure of the web concerning nestedness, clumping, and gradients should be analysed more in detail.
4.2. Additional and supplementary analyses to test nestedness
Pimm and Lawton (1980), Raffaelli and Hall (1992), Bascompte et al. (2003), Bascompte and Jordano (2006), and others point out that food and mutualistic networks are generally nested. This is, however, denied by others (e.g., Paine, 1992; Corbet, 2000; Krause et al., 2003), and, in the case of complex flower-visitor networks (which are characterized by several different taxa of pollinators), by Dicks et al. (2002).
The software Nestedness confirms (with one exception – weakly significant without singletons in 2005) that our web is not nested. The analysis demonstrates that, according to NTC and Binmatnest, significant nestedness of the plant-flower-visitor network is evident, whereas this is not proven by Nestedness. While the discrepancy values d1 also indicate non-nestedness of the system, the same is true for NODF with the exception of 2005. Nestedness shows a noticeable effect of singletons on the evidence of nestedness in 2005; this could be proved by masking the data set.
Data sets of pollination networks published in the literature which, according to NTC or Binmatnest, had shown nestedness (e.g., Dupont et al., 2003), do not show any significant nestedness when re-examined with the software Nestedness and the index d1. This fact is also mentioned by Ulrich (2006a) and Ulrich and Gotelli (2007).
In our dataset, the different methods used to determine nestedness give inconsistent and contradictory results, depending on the null models used. It is impossible to decide which of these results reflect the reality and whether the programs over- or underestimate nestedness. Further methods should be applied to test whether the studied plant-bee web shows nestedness or other web structures. This was carried out by using the “bipartite network”, by modularity tests, and by “multivariate sets (detrended correspondence analysis)”.
4.3. Bipartite graph: interaction structure, linkage levels, abundance, degree of specialization
The visual analyses of the bipartite graph show that the studied network structure is too complex to be assigned to only one of the types (gradient, nested, compartmented, combined types) specified by Lewinsohn et al. (2006) and Almeida-Neto et al. (2007). However, the three methods mentioned by Lewinsohn et al. (2006) are important for pattern recognition. The asymmetry displayed in the bipartite graph shows lower numbers of plant species and higher numbers of bee species. Of all bee species with low interaction numbers and low frequency, most are integrated into network structures by visiting plant species having high interaction numbers and high frequency. The same is true for plant species. The bipartite graph shows an asymmetric pattern of high connectivity, where most of the rare species with low interaction numbers are well integrated into the web. That the most common plant species show the most frequent interactions with bee species and vice versa (the indication for partly nested) might be based on statistical probability. But it is surprising that, although the frequency of polylectic and oligolectic bee species did not differ between the years, there is a significant difference between years according to the interaction numbers of polylectic and oligolectic species. Furthermore, the bipartite graph demonstrates that specialization in flower type is independent of the degree of linkages. According to these results, we can hypothesize that the key factor of our system is the variety of plant resources between years affecting different interaction webs. This should be demonstrated by the modularity degree of the web in 2004 and 2005.
The observed nestedness of the real pollinator web cannot be reproduced by null model 1. Given the significance of both the Shuffle- and the Swap-algorithm in generating temperatures that deviate even if slightly from the observed matrix, both the number of links (constraints of null model 3) and the distribution of marginal totals (constraint of null model 2; i.e., the distribution of common and rare species within the network) need to be taken into account. Thus nestedness is a property of the network rather than of first-order properties alone (Dormann et al., 2009).
4.4. Modularity und functional group correlation
In our plant-bee web, different numbers of modules are visible in both years but nearly identical plant key species mainly influence the module pattern. These plant key species are hub species for those bee species that are present in low numbers and important connector species between modules and separated non-modularized species. An important feature of a hub and connector plant species is high flower density and a specific flower type. The combination of key plant species, which includes the four main flower types (actinomorphic, zygomorphic, Asteroideae-, and Cichorioideae type), guarantees that all bee species – regardless of their body size or their pollen collecting behaviour – will have resources available. The core of the web is structured by hub and connector species, with all other species are gathered around. Corbet (2000) emphasized the importance of various parameters (e.g., flower type, flower size, body size, adaptation to nectar absorption, pollen collecting, and length of the bees’ proboscises) for revealing the compartmentation of a plant-flower-visitor network (see also Kratochwil, 1988). The “detrended correspondence analysis” of our data set shows that these parameters are indeed important features of the structure of the plant-flower-visitor web.
4.5. The consequences for community stability
Bascompte et al. (2003) and Bascompte and Jordano (2006) conclude that mutualistic nested webs are “asymmetric coevolutionary networks”, which guarantee a long-term coexistence of species and facilitate biodiversity maintenance (see Jordano et al., 2003). Consequently, proving that there are non-nested, or only partly nested, patterns within the pollination web would imply that conservation of uncommon and specialist species might not directly be ensured by the existence of generalist species. In our case with current methods, nestedness is essentially impossible to detect, but modularity can be stated as a stabilizing factor which includes partial nestedness.
Which stabilizing features, minimizing the threat of extinction of rare and specialist species in an only partly nested system, can be assumed? As shown in Figure 1, the community structure is (1) dominated by polylectic bee species, and (2) most of the flower-specialized bees depend on floral resources of Fabaceae and Asteraceae species. The species of these families are widespread in our study area, with high abundances. This is also true for large regions in Central Europe, where specialized bees forage on frequently occurring Fabaceae and Asteraceae species (in Germany: 140 oligolectic bee species, 60 of which depend on these two plant families; Kratochwil, 2003). These specialized bee species are highly integrated in the bee-plant web of our study area. Moreover, (3) there are only a few bee species in our system which depend on species of plant families with lower occurrence (e.g., Tetralonia macroglossa on Malva, Osmia adunca on Echium). These species are only slightly integrated within the web structure.
Plant species in our system are not exclusively dependent on one particular bee species. They are also visited by numerous other bee species, which are seldom oligolectic but in most cases polylectic (e.g., Echium vulgare and the specialist Osmia adunca as well as numerous generalists, e.g., several Bombus species). The plant species are visited by higher percentages of generalists than by specialized bee species.
Various analyses have so far shown that the number of bee species in a real web is mostly higher than the number of bee-visited plant species (e.g., Blüthgen et al., 2007). The consequence is that the web structure is asymmetric.
According to the point of view of different authors, only nested communities should guarantee the survival of rare and specialist species by the existence of widely spread generalist species (e.g., Gibson et al., 2006). Recentstudies suggest that nested plant-animal networks are more robust to environmental perturbation (Fortuna and Bascompte, 2006). This would imply that in nested webs the rare and specialist species are just as little endangered as the common generalist species. Our results have shown that under conditions of a partly nested but modularized web, most of the bee species that are characterized by relatively few interactions are connected with those plant species showing the highest degrees of interaction (hub and connector species) and vice versa. Specialized flower visitors are also closely connected with widely distributed and abundant plant species, which are generalists and characterized by a high degree of interaction processes.
Nestedness structure alone does not imply web stability, but modularity includes partly nested subgroups of the web. Although our plant-bee web seems to be structured by an asymmetric pattern and modularity, which produces stability, it should be taken into account that not all rare, specialist, and even oligolectic bee species can always be balanced by the existence of more common and generalist plant species. This is true in our case (e.g., Tetralonia macroglossa, specialist of Malvaceae). Specific analyses of the web structure and functional groups (e.g., body size, pollen-collecting type, flower type) focus on biological traits of community patterns like our studied bee-plant-web.
APPENDIX: ABBREVIATIONS
Plant species: Alyaly: Alyssum alyssoides, Ancoff: Anchusa officinalis, Armmar: Armeria maritima, Berinc: Berteroa incana, Camrap: Campanula rapunculus, Carnut: Carduus nutans, Censto: Centaurea stoebe, Cerarv: Cerastium arvense, Cirarv: Cirsium arvense, Conarv: Convolvulus arvense, Crecap: Crepis capillaris, Cynglos: Cynoglossum officinale, Diacar: Dianthus carthusianorum, Dipten: Diplotaxis tenuifolia, Echvul: Echium vulgare, Erocic: Erodium cicutarium, Eupcyp: Euphorbia cyparissias, Germol: Geranium molle, Helnum: Helianthemum nummularium, Helare: Helichrysum arenarium, Hiepil: Hieracium pilosella, Hypper: Hypericum perforatum, Hyprad: Hypochaeris radicata, Malalc: Malva alcea, Medfal: Medicago falcata, Medmin: Medicago minima, Myoram: Myosotis ramossisima, Onorep: Ononis repens, Papdub: Papaver dubium, Paprho: Papaver rhoeas, Potarg: Potentilla argentea, Pottab: Potentilla tabernaemontani, Salkal: Salsola kali, Salpra: Salvia pratensis, Sedacr: Sedum acre, Senjac: Senecio jacobaea, Senver: Senecio vernalis, Silcon: Silene conica, Sisalt: Sisymbrium altissimum, Starec: Stachys recta, Thypul: Thymus pulegioides, Tradub: Tragopogon dubius, Triarv: Trifolium arvense, Trifcam: Trifolium campestre, Verphl: Verbascum phlomoides, Vicang: Vicia angustifolia, Vicvil: Vicia villosa.
Bee species: Andalf: Andrena alfkenella, Andarg: Andrena argentata, Andbar: Andrena barbilabris, Andbim: Andrena bimaculata, Andcar: Andrena carbonaria agg., Andchr: Andrena chrysosceles, Anddor: Andrena dorsata, Andfal: Andrena falsifica, Andfla: Andrena flavipes, Andmin: Andrena minutula, Andova: Andrena ovatula, Andsub: Andrena subopaca, Andsyn: Andrena synadelpha, Andtib: Andrena tibialis, Antman: Anthidium manicatum, Antlit: Anthidium lituratum, Antpun: Anthidium punctatum, Bomhum: Bombus humilis, Bomlap: Bombus lapidarius, Bompas: Bombus pascuorum, Bompra: Bombus pratorum, Bomsyl: Bombus sylvarum, Bomter: Bombus terrestris, Cercha: Ceratina chalybea, Cercuc: Ceratina cucurbitina, Cercya: Ceratina cyanea, Cherap: Chelostoma rapunculi, Coecon: Coelioxys conoidea, Colcun: Colletes cunicularius, Colfod: Colletes fodiens, Colsim: Colletes similis, Dashir: Dasypoda hirtipes, Epevar: Epeolus variegatus, Halcon: Halictus confusus, Halleu: Halictus leucaheneus, Halpol: Halictus pollinosus, Halqua: Halictus quadricinctus, Halsca: Halictus scabiosae, Halsex: Halictus sexcinctus, Halsma: Halictus smaragdulus, Halsub: Halictus subauratus, Haltum: Halictus tumulorum, Hercre: Heriades crenulatus, Hertru: Heriades truncorum, Hylang: Hylaeus angustatus, Hylann: Hylaeus annularis, Hyldif: Hylaeus difformis, Lasaer: Lasioglossum aeratum, Lasalb: Lasioglossum albipes, Lascal: Lasioglossum calceatum, Lasful: Lasioglossum fulvicorne, Lasgri: Lasioglossum griseolum, Laslatic: Lasioglossum laticeps, Laslat: Lasioglossum lativentre, Lasleu: Lasioglossum leucozonium, Lasluc: Lasioglossum lucidulum, Lasmin: Lasioglossum minutissimum, Lasmor: Lasioglossum morio, Laspau: Lasioglossum pauxillum, Laspra: Lasioglossum prasinum, Laspun: Lasioglossum punctatissimum, Lasvil: Lasioglossum villosulum, Megeri: Megachile ericetorum, Megmar: Megachile maritima, Megpil: Megachile pilidens, Megrot: Megachile rotundata, Megver: Megachile versicolor, Megwil: Megachile willughbiella, Mellep: Melitta leporina, Nomful: Nomada fulvicornis, Nommin: Nomioides minutissimus, Osmadu: Osmia adunca, Osmaur: Osmia aurulenta, Osmleu: Osmia leucomelana, Osmruf: Osmia rufa, Osmspi: Osmia spinulosa, Pancal: Panurgus calcaratus, Rhocan: Rhophitoides canus, Sphalb: Sphecodes albilabris, Sphcri: Sphecodes cristatus, Spheph: Sphecodes ephippius, Sphlon: Sphecodes longulus, Sphmon: Sphecodes monilicornis, Stepun: Stelis punctulatissima, Tetmac: Tetralonia macroglossa.
Acknowledgments
Particular thanks to Till Eggers (University of Osnabrück, Germany) who contributed with important discussions and carried out the bipartite analyses in R-statistics. Heiko Muller (IFOM-IEO Campus, Milan, Italy) enabled us by his support to analyse modularity of our web. Michelle Greve (University of Stellenbosch, South Africa) kindly made the software available to calculate the discrepancy index d1, and Mathew Leibold (University of Texas, USA) the Leibold and Mikkelson software. Thanks also to Bernd Gruber (UFZ Leipzig, Germany) for bipartite and W. Ulrich (University Toru, Poland) for NODF support. We are grateful to A. Schanowski (Bühl/Baden) and to H. Schwenninger (Stuttgart) for checking critical specimens of bee species. We thank the regional administrations for permission to collect specimens. Financial support was provided by the German Federal Environmental Foundation (Deutsche Bundesstiftung Umwelt, Osnabrück).
References
- Almeida-Neto M., Guimarães P.R. Jr., and Lewinsohn T.M. (2007) On nestedness analyses: rethinking matrix temperature and anti-nestedness, Oikos 116, 716–722 [CrossRef] [Google Scholar]
- Almeida-Neto M., Guimarães P., Guimarães P.R. Jr., Loyola R.D., and Ulrich W.A. (2008) A consistent metric for nestedness analysis in ecological systems: reconciling concept and quantification, Oikos 117, 1227–1239 [CrossRef] [Google Scholar]
- Armbrecht I., Tischer I., and Chacon P. (2001) Nested subsets and partition patterns in ant assemblages (Hymenoptera, Formicidae) of Colombian dry forest fragments, Pan-Pac. Entomol. 77, 196–209 [Google Scholar]
- Ashworth L., Aguilar R., Galetto L., and Aizen M.A. (2004) Why do pollination generalist and specialist plant species show similar reproductive susceptility to habitat fragmentation? J. Ecol. 92, 717–719 [CrossRef] [Google Scholar]
- Atmar W., and Patterson B.D. (1993) The measure of order and disorder in the distribution of species in fragmented habitats, Oecologia 96, 373–382 [CrossRef] [PubMed] [Google Scholar]
- Atmar W., Patterson B.D. (1995) The nestedness temperature calculator. A visual basic program, including 294 presence-absence matrices, AICS Research, Inc., University Park, NM and The Field Museum, Chicago. [Google Scholar]
- Barkman J.J., Doing H., and Segal S. (1964) Kritische Bemerkungen und Vorschläge zur quantitativen Vegetationsanalyse, Acta Bot. Neerlandica 13, 394–419 [Google Scholar]
- Bascompte J., Jordano P. (2006) The structure of plant-animal mutualistic networks, in: Pascual M., Dunne J. (Eds.), Ecological networks, Oxford University Press, Oxford, US, pp. 143–159. [Google Scholar]
- Bascompte J., Jordano P., Melián C.J., and Olesen J.M. (2003) The nested assembly of plant-animal mutualistic networks, Proc. Natl Acad. Sci. (USA) 100, 9382–9387 [Google Scholar]
- Beil M., Horn H., and Schwabe A. (2008): Analysis of pollen loads in a wild bee community (Hymenoptera: Apidae) – a method for elucidating habitat use and foraging distances, Apidologie 39, 456–467 [CrossRef] [EDP Sciences] [Google Scholar]
- Bloch C.P., Higgins C.L., and Willig M.R. (2007) Effects of large-scale disturbance on meta-community structure of terrestrial gastropods: temporal trends in nestedness, Oikos 116, 395–406 [CrossRef] [Google Scholar]
- Blüthgen N., Menzel F., Hovestadt T., Fiala B., and Blüthgen N. (2007) Specialization, constraints, and conflicting interests in mutualistic networks, Curr. Biol. 17, 341–346 [CrossRef] [PubMed] [Google Scholar]
- Brualdi R.A., S, and erson J.G. (1999) Nested species subsets, gaps, and discrepancy, Oecologia 119, 256–264 [CrossRef] [PubMed] [Google Scholar]
- Clements F.E. (1916) Plant succession. An analysis of the development of vegetation, Carnegie Institution of Washington, Washington, DC. [Google Scholar]
- Corbet S. (2000) Conserving compartments in pollination webs, Conserv. Biol. 14, 1229–1231 [CrossRef] [Google Scholar]
- Diamond J.M. (1975) Assembly of species communities, in: Cody M.L., Diamond J.D. (Eds.), Ecology and evolution of communities, Harvard Univ. Press, Cambridge Massachusetts, pp. 342–444. [Google Scholar]
- Dicks L.V., Corbet S.A., and Pywell R.F. (2002) Compartmentalization in plant-insect flower visitor webs, J. Anim. Ecol. 71, 32–41 [CrossRef] [Google Scholar]
- Dormann C.F., Fründ J., Blüthgen N., and Gruber B. (2009) Indices, graphs and null models: analyzing bipartite ecological networks, The Open Ecol. J. 2, 7–24 [CrossRef] [Google Scholar]
- Dormann C.F., Gruber B., and Fründ J. (2008) Introducing the bipartite package: analysing ecological networks, RNews 8, 8–11 [Google Scholar]
- Dupont Y.L., Hansen D.M., and Olesen J.M. (2003) Structure of a plant-flower-visitor network in the high-altitude sub-alpine desert of Tenerife, Canary Islands, Ecography 26, 301–310 [CrossRef] [Google Scholar]
- Ejrnaes R. (2000) Can we trust gradients extracted by Detrended Correspondence Analysis? J. Veg. Sci. 11, 565–572 [CrossRef] [Google Scholar]
- Fischer J., and Lindenmayer D.B. (2002) Treating the nestedness temperature calculator as a “black box” can lead to false conclusions, Oikos 99, 193–199 [CrossRef] [Google Scholar]
- Fischer J., and Lindenmayer D.B. (2005) Nestedness in fragmented landscapes: a case study on birds, arboreal marsupials and lizards, J. Biogeogr. 32, 1737–1750 [CrossRef] [Google Scholar]
- Fischer J., and Lindenmayer D.B. (2005) Perfectly nested or significantly nested – an important difference for conservation management, Oikos 109, 485–494 [CrossRef] [Google Scholar]
- Forup M.L., Henson K.S.E., Craze P.G., and Memmott J. (2008) The restoration of ecological interactions: plant-pollinator networks on ancient and restored heathlands, J. Appl. Ecol. 45, 742–752 [CrossRef] [Google Scholar]
- Fortuna M.A., and Bascompte J. (2006) Habitat loss and the structure of plant animal mutualistic networks, Ecol. Lett. 9, 281–286 [CrossRef] [PubMed] [Google Scholar]
- Ganzhorn J.U., and Eisenbeiß B. (2001) The concept of nested species assemblages and its utlility for understanding effects of habitat fragmentation, Basic Appl. Ecol. 2, 87–95 [CrossRef] [Google Scholar]
- Gibson R.H., Nelson L., Hopkins G.W., Hamlett B.J., and Memmott J. (2006) Pollinator webs, plant communities and the conservation of rare plants: arable weeds as a case study, J. Appl. Ecol. 43, 246–257 [CrossRef] [Google Scholar]
- Girvan M., and Newman M.E. (2002) Community structure in social and biological networks, Proc. Natl Acad. Sci. (USA) A99, 7821–7826 [Google Scholar]
- Gleason H.A. (1926) The individualistic concept of the plant association, Bull. Torrey Bot. Club 53, 7–26 [CrossRef] [Google Scholar]
- Greve M., and Chown S.L. (2006) Endemicity biases nestedness metrics: a demonstration, explanation and solution, Ecography 29, 347–356 [CrossRef] [Google Scholar]
- Guimarães P.R., and Guimarães P. (2006) Improving the analysis of nestedness for large sets of matrices, Environ. Modell. Softw. 21, 1512–1513 [CrossRef] [Google Scholar]
- Ibáñez J.J., Caniego J., and García-Álvarez A. (2005) Nested subset analysis and taxa-range size distributions of pedological assemblages: implications for biodiversity studies, Ecol. Model. 182, 239–256 [CrossRef] [Google Scholar]
- Jordano P., Bascompte J., and Olesen J.M. (2003) Invariant properties in coevolutionary networks of plant-animal interactions, Ecol. Lett. 6, 69–81 [CrossRef] [Google Scholar]
- Kent M., Coker P. (1992) Vegetation description and analysis. A Practical Approach, Boca Raton: CRC Press. [Google Scholar]
- Kratochwil A. (1984) Pflanzengesellschaften und Blütenbesuchergemeinschaften: biozönologische Untersuchungen in einem nicht mehr bewirtschafteten Halbtrockenrasen (Mesobrometum) im Kaiserstuhl (Südwestdeutschland), Phytocoenologia 11, 455–669 [Google Scholar]
- Kratochwil A. (1988) Co-phenology of plants and entomophilous insects: a historical area-geographical interpretation, Entomol. Gen. 13, 67–80 [Google Scholar]
- Kratochwil A. (2003) Bees (Hymenoptera: Apoidea) as key-stone species: specifics of resource and requisite utilization in different habitat types, Ber. Reinh.-Tüxen-Ges. 15, 59–77 [Google Scholar]
- Krause A.E., Frank K.A., Mason D.M., Ulanowitz R.E., and Tayler W.W. (2003) Compartments revealed in food web structure, Nature 426, 282–285 [CrossRef] [PubMed] [Google Scholar]
- Leibold M.A., and Mikkelson G.M. (2002) Coherence, species turnover, and boundary clumping: elements of meta-community structure, Oikos 97, 237–250 [CrossRef] [Google Scholar]
- Lewinsohn T.M., Ináco Prado P., Jordano P., Bascompte J., and Olesen J.M. (2006) Structure in plant-animal interaction assemblages, Oikos 113, 174–184 [CrossRef] [Google Scholar]
- Memmott J. (1999) The structure of a plant-pollinator food web, Ecol. Lett. 2, 276–280 [CrossRef] [Google Scholar]
- Muller H. (2008) Identification and analysis of co-occurrence networks with NetCutter. – NetCutter 1.0 software documentation. [Google Scholar]
- Olesen J.M., Eskildsen L.I., and Venkatasamy S. (2002) Invasion of oceanic island-pollination networks: importance of invader complexes and endemic super generalists, Diversity and Distribution 8, 181–192 [CrossRef] [Google Scholar]
- Olesen J.M., Bascompte J., Dupont Y.L., and Jordano P. (2008): The modularity of pollination networks, PNAS 104, 19891–19896 [CrossRef] [Google Scholar]
- Ollerton J., Johnson S.D., Cranmer L., and Kellie S. (2003) The pollination ecology of an assemblage of grassland asclepiads in South Africa, Ann. Bot. 92, 807–834 [CrossRef] [PubMed] [Google Scholar]
- Paine R.T. (1992) Food-web analysis through field measurement of per capita interaction strength, Nature 355, 73–75 [CrossRef] [Google Scholar]
- Patterson B.D., and Atmar W. (1986) Nested subsets and the structure of insular mammalian faunas and archipelagos, Biol. J. Linn. Soc. 28, 65–82 [CrossRef] [Google Scholar]
- Philipp M., Böcher J., Siegismund H.R., and Nielsen L.R. (2006) Structure of a plant-pollinator network ona pahoehoe lava desert of the Galápagos Islands, Ecography 29, 531–540 [CrossRef] [Google Scholar]
- Pimm S.L., and Lawton J.H. (1980) Are food webs divided into compartments? J. Anim. Ecol. 49, 879–898 [CrossRef] [Google Scholar]
- R Development Core Team (2008) R: A language and environment for statistical computing R. – Foundation for Statistical Computing, Vienna, Austria. ISBN 3-900051-07-0, URL http://www.R-project.org. [Google Scholar]
- Raffaelli D., and Hall S. (1992) Compartments and predation in an estuarine food web, J. Anim. Ecol. 61, 551–560 [CrossRef] [Google Scholar]
- Rodriguéz-Gironés M.A., and Santamaría L. (2006) A new algorithm to calculate the nestedness temperature of presence-absence matrices, J. Biogeogr. 33, 924–935 [CrossRef] [Google Scholar]
- Simberloff D. (1983) Competition theory, hypothesis testing, and other community ecological buzzwords, Am. Nat. 122, 626–635 [CrossRef] [Google Scholar]
- Tilman D. (1982) Resource competition and community structure, Princeton Univ. Press, Princeton. [Google Scholar]
- Ulrich W. (2006a) Nestedness – a FORTRAN program for calculating ecological matrix temperatures. [Google Scholar]
- Ulrich W. (2006b) CoOccurence – a FORTRAN program for species co-occurrence analysis. [Google Scholar]
- Ulrich W., and Gotelli N.J. (2007) Null model analysis of species nestedness patterns, Ecology 88, 1824–1831 [CrossRef] [PubMed] [Google Scholar]
- Vázquez D.P., and Aizen M.A. (2004) Asymmetric specialization: a pervasive feature of plant-pollinator interaction, Ecology 85, 1251–1257 [CrossRef] [Google Scholar]
- Walter H., Lieth H. (1967) Klimadiagramm Weltaltlas, VEB Gustav Fischer Verlag, Jena. [Google Scholar]
- Waser N.M., Chittka L., Price M.V., Williams N.M., and Ollerton J. (1996) Generalization in pollination systems and why it matters, Ecology 77, 1043–1060 [CrossRef] [Google Scholar]
All Tables
Coherence as indicated by the occurrence of embedded absences in ordinated matrices; species turnover as indicated by the number of times one species replaces another between two sites, and boundary clumping as indicated by Morisita’s Index (Leibold and Mikkelson, 2002).
Nested subset-analysis of the pollination web calculated via NTC (Atmar and Patterson, 1995), BINMATNEST (Rodriguéz-Gironés and Santamaría, 2006) and NESTEDNESS (Ulrich, 2006a), T = temperature in degrees, Trandom = randomized mean temperature (1000 iterations), N = degree of nestedness, P = level of significance.
Discrepancy indices: “BR” (Brualdi and Sanderson, 1999), “NODF” (Almeida-Neto et al., 2008) and “d1” (Greve and Chown, 2006), BRSim, NODFSim = randomized value (1000 iterations), P = significance level.
Temperature of nestedness analysed by The bipartite Package 0.73 (Dorman et al., 2008) for the data set of 2005: real data, null-model 1 (Patefield algorithm), null-model 2 (Shuffle) and null-model 3 (swap-algorithm).
Modularity degrees of the real data sets (2004, 2005), of the 50 randomized graphs by edge-swapping (1000 iterations) according to NetCutter 1.0 (Muller, 2008).
Web modules in 2004 and 2005 according to NetCutter 1.0 (Muller, 2008) analysed with edge-betweeness clustering. In parenthesis species numbers; key hub and connector plant species in bold and italics. N = number of interactions. For abbreviations of plant species, see Appendix.
All Figures
 |
Figure 1 Web structure (bipartite graph) of the studied plant-bee system in 2004 (a) and 2005 (b). S = specialization (flower types: A = actinomorphic, Z = zygomorphic, AS= Asteroideae, CI = Cichorioideae; pollen collecting: P = polylectic, oligolectic in Asteraceae = AST, Boraginaceae = BOR, Fabaceae = FAB, Malvaceae = MAL, Salicaceae = SAL; C = cuckoo bees); Lm = plant linkage level; ln: relative plant linkage level; D = distribution; number of plots with occurrence; B = body size group (a = small [ < 10 mm], b = medium [ > 10–12 mm], c = large (> 12 mm)); Lm = bee linkage level; ln: relative bee linkage level lm. For abbreviations of plant and bee species, see Appendix. |
| In the text | |
 |
Figure 2 Modularity graph (Software NetCutter 1.0; Muller, 2008) of 2004 and 2005, which is based on edge-betweenness clustering (further explanations see text). |
| In the text | |
 |
Figure 3 Detrended correspondence analysis of the plant-bee web 2004 with plant species (a) and bee species (b) plotted by PC-ORD 5.0 and characterization by flower types and bee body sizes. Key hub and connector plant species in bold and italics. For abbreviations of plant species, see Appendix. |
| In the text | |


